Magneto Optical Trap Modelling

Background

The magneto-optical trap (MOT) is one the most effective platforms in experimental atomic physics and has become a widely used technique in academic research and R&D departments around the globe. Cold atom clouds resulting from laser cooling and trapping of neutral atoms are key to precision measurements in a wide range of physical observables. Advances in atomic clocks, quantum communication, quantum computing, atomic gravimetry and ground-breaking advances in science such as Bose-Einstein Condensation can be attributed to the development of magneto-optical trapping.

A majority of cold-atom experiments start with the use of an MOT to cool and trap the atoms by using the effects of radiation pressure from a red-detuned laser beam. The efficacy of these cold ensembles has a strong dependency on the number of atoms trapped and the velocity distribution, as this will improve the signal-to-noise ratio of any particular experiment. It remains a challenge to capture the full picture of the atomic dynamics, which is why we have developed a simple model to perform multivariable optimisation to rely less on human intuition and increase the overall efficiency of a standard MOT setup. It is crucial to understand the scaling laws that govern the behaviour of these cold atom clouds to find how the number of atoms, and the capture velocity can be maximised with the availability of larger laser power in the relevant wavelengths.

In a one-dimensional MOT, a pair of counter-propagating circularly polarised laser beams interact with an atomic cloud of alkali metal gas. Each laser is red-detuned from the atomic resonance frequency of the substance and a magnetic gradient is generated to Zeeman split the transitions to create a spatially dependent trapping force. The atoms are Doppler cooled by the red-detuned lasers and the Zeeman shift ensures that the atoms are pushed towards the centre of the trap, where the magnetic field is zero.

Magneto Optical Traps

The key benefit of the MOT is that it introduces a spatially dependent scattering force by using the magnetic hyper-fine transitions, or Zeeman effect of the atom-light interaction.

The Zeeman splitting of $\mathbf{F}$ levels into $2\mathbf{F}+1$ can be studied in our one-dimensional model. Consider the ground state $F = 0, m_F = 0$ and excited state $F = 1, m_F = -1, 0, 1$ of an atom. When this system is in the presence of a magnetic gradient the resonant frequency will change with its position as the atom travels.

In a standard 6-beam MOT we have three sets of counter-propagating laser beams red-detuned from the resonant frequency of the atoms with the same circular polarisation. In this scheme, the first laser denoted $L_1$ will drive $\sigma^+$ transitions when it is parallel to the magnetic field vector $\mathbf{B}$, and $\sigma^-$ transitions when it is anti-parallel to $\mathbf{B}$. As the atoms travel towards one of the lasers, the probability of absorbing a photon from it increases. This creates a scattering force that accelerates the atoms towards the centre of the trap where a balance of the forces is achieved.

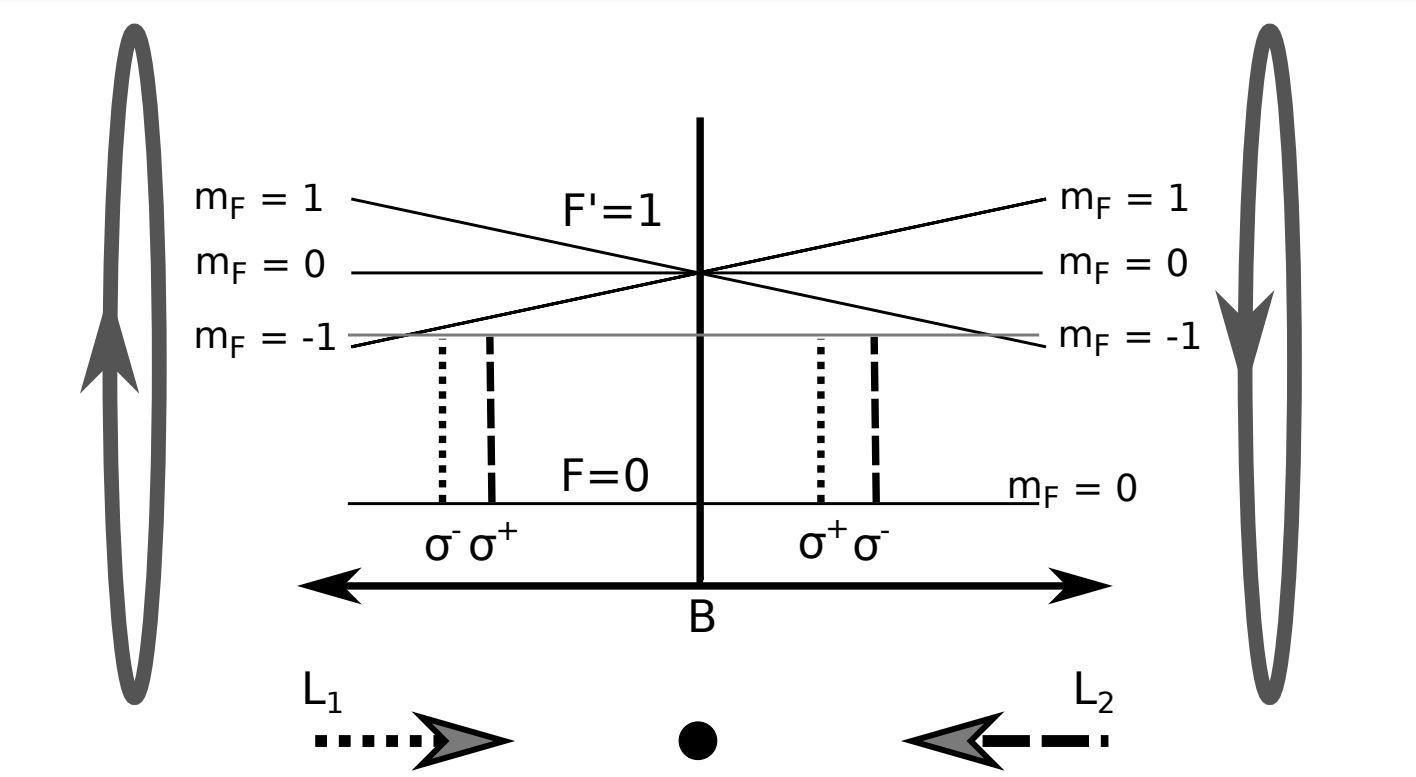
The quadrupole magnetic field $\mathbf{B} = {x, y, -2z}$ produces the position-dependent splitting of the Zeeman levels. In order to account for this in the model, we consider the corresponding change of frequency in the transition $\Delta_\pm = \Delta \pm \vec{k} \cdotp \vec{v} \mp \mu’ B /\hbar$ where $\mu ‘ = (g_e m_e - g_g m_g)\mu_B$ is the effective magnetic moment of the transition, $\mu_B$ is the Bohr magneton, $g$ is the Landé g-factor and $m$ the magnetic number of the state.

Computational Model

We use a quasi-one-dimensional model to study the behaviour of the standard 6-beam MOT. It treats the laser beam as having a uniform intensity profile and the atom as a two-level system. It is able to predict most of the trends found experimentally quite accurately.

We predict the steady state number of atoms $N_A$ that is trapped by treating the capture volume as a sphere with radius $r$, equal to the beam radius of the trapping laser. Using the 1D force equation, we can calculate the flux of the atoms inside the trapping region which have a speed lower than the capture velocity $v_c$. The number of atoms trapped by an MOT can be calculated as shown by Monroe et al.

where $R$ is the capture rate, $1/\tau_{trap}$ the loss rate due to collisions with the background gas and $v_t = \sqrt{2 k_B T/m}$ the thermal velocity of the background vapour. The collision cross-section for the $^{87}Rb$ atoms $\sigma$ is the area around a given atom which the centre of another atom must reach to cause a collision. This is estimated to be around $\sigma = 2 \times 10^{-17}$m$^2$.

Using the Runge-Kutta methods of integration (RK45), we can solve the differential equation for the acceleration:

to find the capture velocity $v_c$, such that $x(v_c) = 2r$, as a function of beam radius $x$, beam intensity $I$, detuning $\Delta$ and magnetic field gradient $B$, and the steady state number of atoms trapped.

We can see here the numerical solution for the simulation for a laser beam with a radius of 1cm and varying magnetic field gradient.

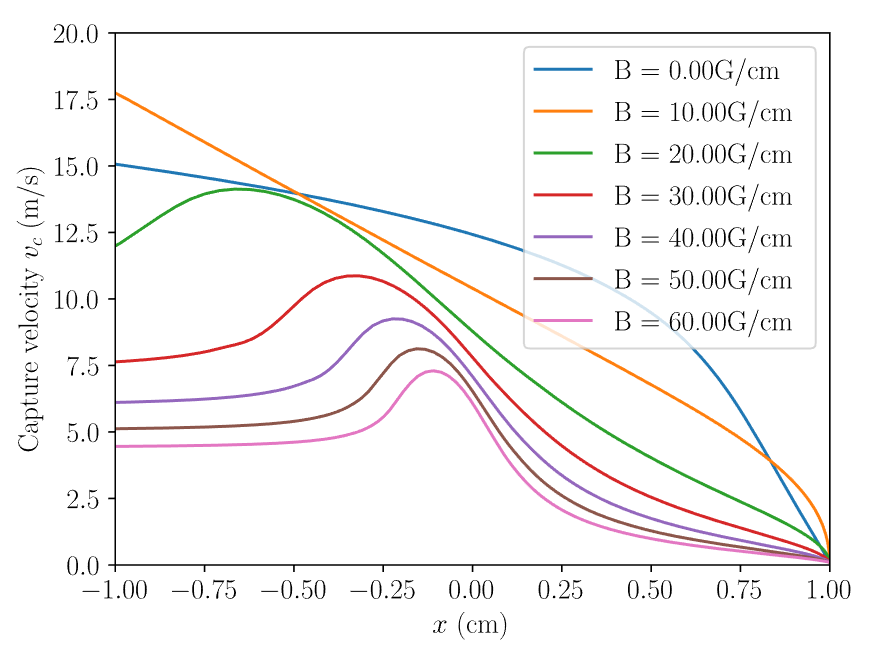
With this simple model we were able to create a function that finds the optimal parameters to maximise the number of atoms trapped. Using the scipy package in Python we minimised the inverse of the scalar function $N_A(x, I, \Delta, B)$ where $x$ is the beam radius. We choose a suitable first guess and the relevant boundaries for the multi-parameter optimisation function. This gives us the maximum number of atoms trapped based on our chosen parameters. And we can see how the number of atoms varies with the trap parameters, with all parameters reaching a peak $N_A$ for a given beam diameter.

Grating Magneto-Optical Trap

The GMOT is a magneto-optical trap that uses surface-patterned chips to diffract a single input laser beam to form a laser overlap volume that is able to trap an atom cloud. It was first proposed by Vangeleyn et al. in order to achieve the miniturisation of MOTs, a highly desirable device both for AMO research and high-precision atomic clocks.

The chips are comprised of three linear gratings at 120 degrees relative to their planes. The Bragg condition applies to the diffracted beams as such:

where $d_g$ is the period of the grating, $\theta$ the diffraction angle and $\lambda$ the wavelength of the beam.

The total number of atoms trapped $N_A$ depends on the laser frequency, intensity and overlap volume. After further development of the coated grating with industrial partners, the team was able to build a trap with micro-fabricated optics which could trap up to $6 \times 10^7$ atoms.